Tiny Tapeout is an educational project that makes it easier and cheaper than ever to get your designs manufactured on a real chip! Instead of paying 10,000 dollars for taping out a chip, enthusiasts and hobbyists can submit designs and share the floorplans in the same chips, dramatically reducing the per-design cost for individuals.
The final chip product shipped to me will include a chip on a carrier board and a demo board to communicate with the chip.

Since I have completed ChipCraft‘s 8-bit calculator course (Slide 157 Lab ID: C-EQUALS), I decided to submit this design to the Tiny Tapeout 8th iteration (TT8), which is due on September 6, 2024.
Because my design is coded with TL-Verilog, I followed Steve Hoover‘s tt08-makerchip-template and the 5-minute YouTube tutorial, which are extremely helpful.
My submitted TT8 design can be found at ezchips/tt08-my-calc (github.com) repository.
During the process of compiling my design, I did run into GDS Build issue with the following error:
/home/runner/work/tt08-my-proj/tt08-my-proj/src/project.sv:124: ERROR: Identifier `\L1_Digit[0].L2_Leds[0].L2_viz_lit_a0' is implicitly declared and `default_nettype is set to none.
Steve provided me with a neat trick by adding `default_nettype wire to the first \SV region of the project.tlv file, and it worked beautifully.
Here is the snapshot of a successful submission reported by TT08’s discord group:

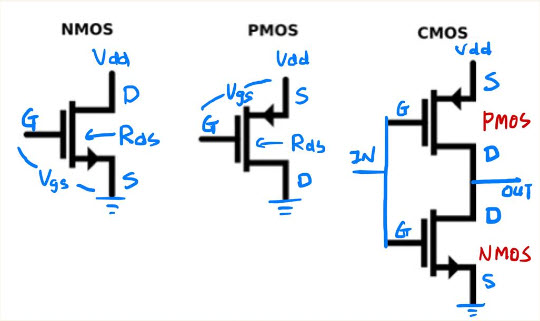
It is really cool to have a 2D and 3D view of my design’s floor plan in the chip, which includes many semiconductor components like gates, flip-flops, multiplexers, etc.